新型コロナPCR検査にベイズの定理を用いることの不適切さは何度も記事にしました。



1年経っても未だにベイズの定理の論争が続いています。
そろそろ終止符を打ちましょう。
Contents
ベイズの定理を用いた計算
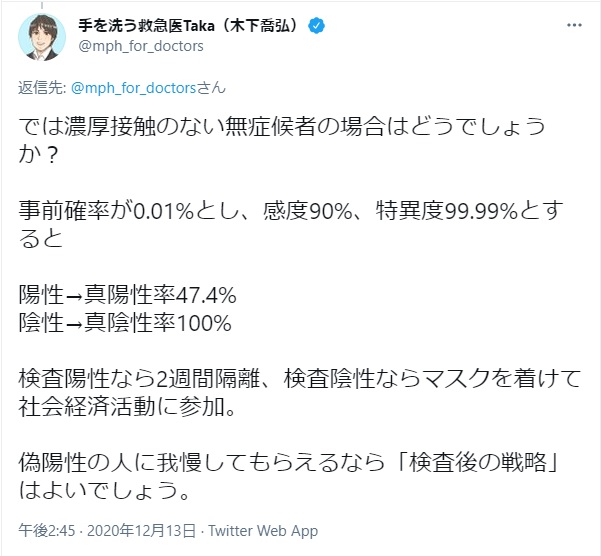
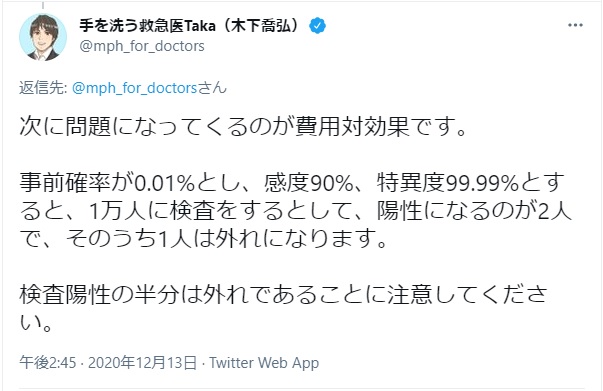
この計算には問題があります。
事前確率の計算と隠された仮定
事前確率はどのようにして求めるのでしょうか?
本当にPCR検査は必要か?
まずは、日本に新型コロナの患者さんがどれくらいいるのか考えてみましょう。2020年5月10日時点の日本の感染者は延べ15847人。ここから回復した8293人、死亡した633人を減ずれば、現段階で感染状態にあるのは6921人ということになります。
しかし、専門家の中にも、実際にはこの10倍から20倍の患者がいてもおかしくないという意見もあります。多めに見積もって、仮に20倍とすると、日本には138420人の感染状態の人がいるということになります。日本の人口は1.265億人ですから、913人に1人が感染状態にある可能性がある、ということになります。
ここでは計算しやすくするために1000人に1人が感染状態であると仮定します。
https://www.yushoukai.org/blog/pcr
つまり、日本における新型コロナの「有病率」は0.1%ということになります。
医療法人社団悠翔会 佐々木淳氏
編集Y:仮に東京都民1000万人(※実際には推計1398万人です)が全員検査を受けたとしますよね。現在のPCR検査の陽性率が5%(7日間移動平均、データはこちら)ですから、仮にこれをそのまま当てはめて、50万人いたとしましょう(これはあくまで計算上の仮定です、ご注意ください)。……で、全員検査を受けても、このうちの3割が偽陰性になるわけですか。15万人の陽性の人が、自分の感染に気づけず、診療・隔離もされないことになりますね。
https://business.nikkei.com/atcl/gen/19/00164/052700002/?P=2&mds
峰 宗太郎氏
事前確率の計算は次の通りです。
(罹患率、陽性率をそのまま事前確率として用いることが多いようです)
事前確率 = 陽性者数 / 検査数(人口) × 100
(「陽性者数」は新型コロナPCR検査で確定した陽性者数)
ここで新型コロナPCR検査の特異度を100%未満と考える場合、真の陽性者数はPCR検査で確定した陽性者数よりも少なくなるはずです。(感度、検査の充足度等を無視した場合)
従って事前確率を求める場合には特異度による補正が必要となります。
事前確率を求める段階で特異度が不定であれば事前確率を求めることは不可能です。
ところが上記の式には特異度は出てきませんし、佐々木氏、峰氏が特異度による補正を行っているようには見えません。
事前確率を求める際、暗黙的に新型コロナPCR検査の特異度を100%と仮定して使用していると考えられます。
(事前確率を求める場合、感度による補正や検査の充足度を考慮しての補正も必要です。上記の佐々木氏は検査の充足度を考慮しての補正をしているように見えます。佐々木氏は陽性者の20倍の感染者がいると仮定しながら、検査抑制論を主張する不思議な人です)
暗黙的に新型コロナPCR検査の特異度を100%と仮定することについて
暗黙的に新型コロナPCR検査の特異度を100%と仮定することは間違ったことではありません。
日々報告されている新型コロナの陽性者数、陽性率、実行再生産数等の感染指標も特異度100%の前提を置いています。
新型コロナの分科会が作成している資料も新型コロナPCR検査の特異度を暗黙的に100%と仮定しています。(PCR陽性率、新規陽性者数)
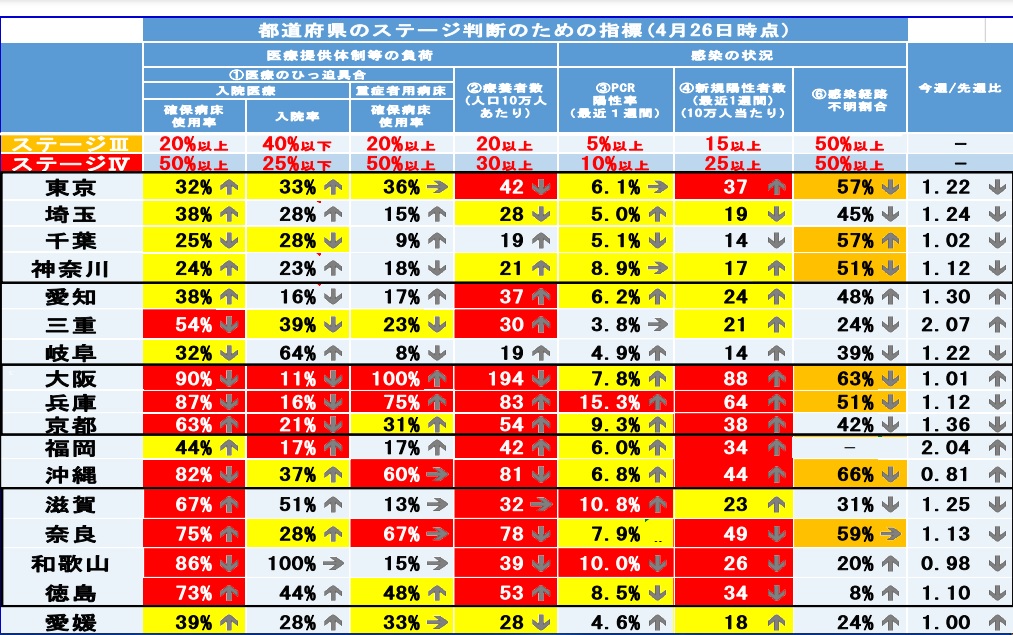
https://corona.go.jp/emergency/pdf/status-medical-care_20210427.pdf
1つの式の中に異なる2つの特異度が存在
ベイズの定理を用いて事後確率(陽性一致率)を求める場合、事前確率と仮定した特異度を使用します。
ところが事前確率を求める際に暗黙的に特異度を100%として使用しているため、1つの式の中に異なる2つの特異度が存在することになります。
当然ですがこのようなことは数学では行ってはいけません。
従って新型コロナPCR検査にベイズの定理を用いてはいけません。
もう少し詳しく説明します。
事前確率の正しさを保証するのが新型コロナPCR検査
峰氏のように陽性率をそのまま事前確率とする人がいます。
事前確率の正しさは何によって保証されているのでしょうか?
この場合、峰氏は新型コロナPCR検査の特異度(感度)を暗黙的に100%と仮定していると考えられます。
仮に新型コロナPCR検査の感度、特異度が非常に低いものであった場合は陽性率をそのまま事前確率とすることはできません。
わかりにくい場合は新型コロナPCR検査の感度、特異度を70%程度と仮定し、陽性率から事前確率を求めるための式を考えてみて下さい。
事前確率を求める式の中に必ず特異度(感度)が入る事がわかると思います。
特異度が99.9%であろうが、99.999999%であろうが議論は大きくは変わりません。
特異度を100%と仮定する場合は式の中に特異度は必要無くなりますが、特異度を仮定していることに変わりはありません。
つまり、事前確率を求める段階で新型コロナPCR検査の特異度が不定であれば事前確率を求めることは不可能ですので特異度は既に決まっているはずです。
事前確率を求める段階で特異度を仮定しておきながら、事後確率を求める際に再度、特異度を仮定するというおかしなことを行っているのです。
事前確率を求める段階でPCR検査の感度、特異度の高さで事前確率の正しさを保証した上でPCR検査よりも感度、特異度が劣る抗原検査や抗体検査の有効性を調べるのがベイズの定理の正しい使い方です。
事前確率を求めるために新型コロナPCR検査の特異度を100%として用い、抗原検査や抗体検査の特異度を99%として仮定する場合はベイズの定理を用いることはできると考えます。 (通常はこのような使い方をするはずです)
まとめると
新型コロナPCR検査妨害論者は日々報告されている新型コロナの陽性者数、陽性率、実行再生産数等については暗黙的に新型コロナPCR検査の特異度を100%と仮定して扱っておきながら、大量検査の議論をする際に限り特異度を100%未満の数字に設定します。
ベイズの定理を用いる際、事前確率の計算で暗黙的に特異度を100%として使用しているため、1つの式の中に異なる2つの特異度が存在することになっています。
新型コロナPCR検査妨害論者は事前確率を重視すると主張します。
ところが事前確率を求めるための計算式が明示されたことはただの一度もありません。
嘘がバレるからでしょう。
一体いつまでデタラメな議論を続けるつもりでしょうか?











