コロナウイルスPCR検査を行う場合に事前確率が低いと考えられる場合には検査を行うべきではないと主張する人達がいます。
その理由としてベイズの定理を用いた計算で事後確率が低くなるからとしています。
本当なのでしょうか?
事後確率の計算方法
動画を説明しますと
有病率0.1%、精度(感度、特異度)99%、10万人に検査を行った場合
本当に病気に罹患している人は100人、罹患していない人は99900人。
本当に病気に罹患している人で陽性と判定される人は99人、陰性と判定される人は1人。
罹患していない人で陽性と判定される人は999人、陰性と判定される人は98901人。
陽性と判定された場合に本当に陽性の確率は99/99+999 = 11/122 = 約9%(事後確率)
従って事前確率が低い場合は検査を行ってはならない。
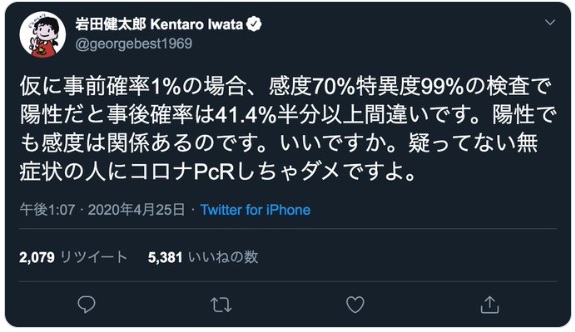
岩田先生も数字は異なりますが同じようなことを言ってます。
PCR検査の特異度
厚生労働省の資料によると調査したコロナウイルスPCR検査キットの特異度はいずれも100%でした。 (https://www.niid.go.jp/niid/images/lab-manual/2019-nCoV-17-current.pdf)
検体採取のタイミングやウイルス量が原因で偽陰性は起こり得ると思います。しかし存在しないものを生み出すことはできないので検体採取時の手技が問題で偽陽性は通常起こり得ません。偽陽性が起こりうるのは人為的なミス以外はあまり考えられません。従ってPCR検査の特異度はほぼ100%と考えても良いと思います。
ちなみに猫伝染性腹膜炎でのPCR検査の感度は98.7%、特異度は100%です。

Mycoplasma感染症診断におけるLAMP法(PCR検査と同様に遺伝子を増幅させて検査する検査法)の感度は95%、特異度は100%です。 http://www.jscm.org/journal/full/02302/023020087.pdf
上記の計算の問題点
上の動画では何故か計算時には感度、特異度という言葉を使わず精度という言葉を使っています。精度99%ということで非常に高精度の検査のように思います。
一般的な検査に関しては上記の計算方法でも問題は無いと思います。
しかしPCR検査の特異度について、ほぼ100%を99%として計算しても良いのでしょうか?
感度90%、特異度99.9%、特異度99.99%、特異度99.999%として計算した場合
特異度を99.9%、99.99%、99.999%として計算しました。特異度を上げたので感度は少し下げました。
有病率0.1%、感度90%、特異度99.9%、10万人に検査を行った場合
本当に病気に罹患している人は100人、罹患していない人は99900人。
本当に病気に罹患している人で陽性と判定される人は90人、陰性と判定される人は10人。
罹患していない人で陽性と判定される人は99人、陰性と判定される人は99801人。
陽性と判定された場合に本当に陽性の確率は90/90+99 =90/189 = 約48% (事後確率)
有病率0.1%、感度90%、特異度99.99%、10万人に検査を行った場合
本当に病気に罹患している人は100人、罹患していない人は99900人。
本当に病気に罹患している人で陽性と判定される人は90人、陰性と判定される人は10人。
罹患していない人で陽性と判定される人は9人、陰性と判定される人は99891人。
陽性と判定された場合に本当に陽性の確率は90/90+9 =90/99 = 約91% (事後確率)
有病率0.1%、感度90%、特異度99.999%、10万人に検査を行った場合
本当に病気に罹患している人は100人、罹患していない人は99900人。
本当に病気に罹患している人で陽性と判定される人は90人、陰性と判定される人は10人。
罹患していない人で陽性と判定される人は1人、陰性と判定される人は99899人。
陽性と判定された場合に本当に陽性の確率は90/90+1 =90/91 = 約99% (事後確率)
有病率が低くても特異度が高い場合は事後確率は高くなります。
まとめると
検査の有用性を考える場合、PCR検査のような精度が高い検査の特異度を99%という低い数値に設定してしまうのは不適切です。
特異度99%を99.9%、99.99%、99.999%とするだけで計算結果は大きく変わります。
特異度を99%として計算しているのはPCR検査の原理を理解していないのでしょう。
下記サイトを参考にさせて頂きました。
PCR検査阻止理論の詐欺話法
http://onodekita.sblo.jp/article/187506017.html
1ミリの物体の長さを測ろうと思うときに、1メモリが1センチ(10倍)の定規を持ってきて、定規ではうまく測れないから、定規で測るのは無意味だと主張する。












